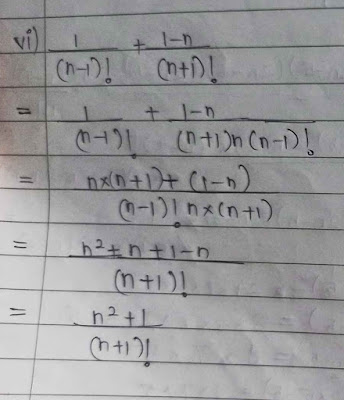EXERCISE 3.2
1. Evaluate:
(i) 8!
=8×7×6×5×4×3×2×1
=40320
(ii)10!
=10×9×8×7×6×5×4×3×2×1
=3628800
(iii)10!-6!
=10×9×8×7×6!-6!
=6!(10×9×8×7-1)
=3628080
(iv) (10-6)!
=4!
=4×3×2×1
=24
2. Compute
(i) `\frac{\text{12!}}{\text{6!}}`
= `\frac{\text{12!}}{\text{6!}}`
=` \frac{\text{12x11x10x9x8x7x6!}}{\text{6!}}`
=12×11×10×9×8×7
=665280
(ii)`\left(\frac{\text{12}}{\text{6}}\right)!`
= `\left(\frac{\text{12}}{\text{6}}\right)!`
= 2!
=2
(iii) (3×2)!
= 6!
=6×5×4×3×2×1
=720
(iv) 3!×2!
= 3×2×1×2×1
=12
(v)` \frac{\text{9!}}{\text{3! 6!}}`
=`\frac{\text{9 8 7 6!}}{\text{3! 6!}}`
=`\frac{\text{504}}{\text{6}}`
=84
(vi)`\frac{\text{6!-4!}}{\text{4!}}`
=`\frac{\text{6×5×4!-4!}}{\text{4!}}`
=`4!\left(\frac{\text{6×5-1}}{\text{4!}}\right)`
=30-1
=29
(vii)`\frac{\text{8!}}{\text{6!-4!}}`
=`\frac{\text{8×7×6×5×4!}}{\text{6×5×4!-4!}}`
=`\frac{\text{4!}}{\text{4!}}\left(\frac{\text{8×7×6×5}}{\text{6×5-1}}\right)`
=`\frac{\text{1680}}{\text{30-1}}`
=57.93
(viii)`\frac{\text{8!}}{\text{(6-4)!}}`
=`\frac{\text{8!}}{\text{(6-4)!}}`
=`\frac{\text{8×7×6×5×4×3×2!}}{\text{2!}}`
=40320
3. Write in terms of factorials
(i)5×6×7×8×9×10
`=\frac{\text{10×9×8×7×6×5×4×3×2×1}}{\text{4×3×2×1}}`
`=\frac{\text{10!}}{\text{4!}}`
(ii)3×6×9×12×15
=1×3×2×3×3×3×4×3×5×3
=1×2×3×4×5×3×3×3×3×3
`=5!×3^{5}`
(iii)6×7×8×9
` =\frac{\text{9×8×7×6×5×4×3×2×1}}{\text{5×4×3×2×1}} `
`=\frac{\text{9!}}{\text{5!}}`
(iv) 5×10×15×20
=1×5×2×5×3×5×4×5
`=4!×5^{4}`
4. Evaluate
$\frac{n!}{r!(n-r)!}$ for
(i) n=8, r=6 (i) n=12, r=12 (i) n=15, r=10 (i) n=15, r=8
solution:
(i)`\frac{\text{8!}}{\text{6!(8-6)!}}`
=`\frac{\text{8×7×6!}}{text{6!2!}}`
$=\frac{56}{2}=28$
(ii) `\frac{\text{12!}}{\text{12!(12-12)!}}`
=`\frac{\text{1}}{\text{0!}}`
=1
(iii)`\frac{\text{15!}}{\text{10!(15-10)!}}`
=`\frac{\text{151413121110!}}{\text{10!5!}}`
=`\frac{\text{360360}}\{\text{120}}`
=3003
(iv) `\frac{\text{15!}}{\text{8!(15-8)!}}`
=`\frac{\text{15×14×13×12×11×10×9×8!}}{\text{8!5!}}`
=`\frac{\text{32432400}}\{\text{120}}`
=270270
5. Find n, if
(i)`\frac{\text{n}}{\text{8!}}=\frac{\text{3}}{\text{6!}}+\frac{\text{1!}}{\text{2!}}`
`\frac{\text{n}}{\text{8!}}=\frac{\text{3 4!+6!}}{\text6!4!}`
`\frac{\text{n}}{\text{8!}}=4!\frac{\text{3+6 5}}{\text{6!4!}`
`\frac{\text{n}}{\text{8!}}=\frac{\text{3+30}}{\text{6!}}`
`\frac{\text{n}}{\text{8!}}=\frac{\text{33}}{\text{6!}}`
`n=\frac{\text{33×8×7×6!}}{\text{6!}}`
`n=1848`
(ii)`\frac{\text{n}}{\text{6!}}=\frac{\text{4}}{\text{8!}}+\frac{\text{3}}{\text{6!}}`
`\frac{\text{n}}{\text{6!}}=\frac{\text{4 6!+3×8!}}{\text{8!6!}}`
`\frac{\text{n}}{\text{6!}}=\frac{\text{6!(4+3×8×7)}}{\text{8!6!}}`
`n=\frac{\text{4+3×8×7}}{\text{8×7}}`
`=\frac{\text{4(1+3×8×7)}}{\text{8×7}}`
`=\frac{\text{1+42}}{\text{14}}`
`=\frac{\text{43}}{\text{14}}`
6. Find n if :
(i)`\frac{\text{(17-n)!}}{\text{(14-n)!}`=5!
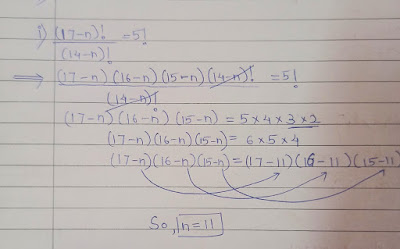 |
| Factorial Notation 11th Class Maharashtra Board EXERCISE 3.2 |
(iii)`\frac{\text{n!}}{\text{3!(n-3)!}}:\frac{\text{n!}}{\text{5!(n-5)!}}=5:3`
(iv)`\frac{\text{n!}}{\text{3!(n-3)!}}:\frac{\text{n!}}{\text{5!(n-7)!}}=1:6`
(v)`\frac{\text{n!}}{\text{3!(n-3)!}}:\frac{\text{n!}}{\text{5!(n-5)!}}=24:1`
8. Show that
`\frac{\text{n!}}{\text{r!(n-r)!}}+\frac{\text{n!}}{\text{(r-1)!(n-r+1)!}}=\frac{\text{(n+1)!}}{\text{r!(n-r+1)!}}`
9. Show that
Factorial Notation 11th Class Maharashtra Board EXERCISE 3.2
10.Simplify
(i)`\frac{\text{(2n+1)!}}{\text{(2n)!}}`
(ii)$\frac{(n+3)!}{(n^2-4)(n+1)!}$
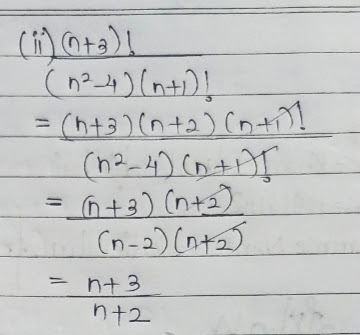 |
| Factorial Notation 11th Class Maharashtra Board EXERCISE 3.2 |
(iii)`\frac{\text{1}}{\text{n!}}-\frac{\text{1}}{\text{(n-2)!}}`
(iv) $n[n!+(n-1)!]+n^{2}(n-1)!+(n+1)!$
 |
| Factorial Notation 11th Class Maharashtra Board EXERCISE 3.2 |
(v)`\frac{\text{n+2}}{\text{n!}}-\frac{\text{3n+1}}{\text{(n+1)!}}`
(vi)`\frac{1}{(n-1)!}+\frac{\text{1-n}}{\text{(n+1)!}}`
(vii)`\frac{1}{n!}-\frac{3}{(n+1)!}-\frac{n^2-4}{(n+2)!}`
(viii)$\frac{n^2-9}{(n+3)!}+\frac{6}{(n+3)!}-\frac{1}{(n+1)!}$
 |
| Factorial Notation 11th Class Maharashtra Board EXERCISE 3.2 |
Maharashtra Board EXERCISE 3.2
Written by Javeda , edit By Mukesh