Sets relation function operation on set

Operation ON SETS

1) Complement of a set:

The complement of the set A is denoted by

A' or Ac .It is defined as

A' = {x/x∈U, x∉A} = set of all elements in

U which are not in A.

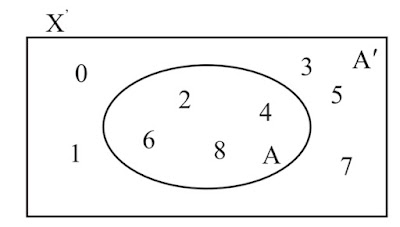
Ex. Let X = {0, 1, 2, 3, 4, 5, 6, 7, 8} be the

Universal Set and A = {2, 4, 6, 8}

Sets relation function operation on set

∴ The complement of the set A is

A' = {0, 1, 3, 5, 7}

Properties:

i) (A')' = A ii) φ' = U iii) U' = φ

2) Union of Sets:

The union of two sets A and B is the set of

all elements which are in A or in B, (here

'or' is taken in the inclusive sense) and is

denoted by A ∪ B

Thus, A ∪ B = {x/x∈A or x∈B}

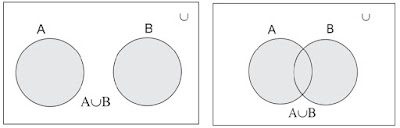
The Union of two sets A and B i.e.

A ∪ B is represented by a shaded part in

Venn-diagram as in

Sets relation function operation on set

Ex. A = {x/x is a prime number less than 10}

B= {x/x∈N, x is a factor of 8}

find A∪B.

Solution :

We have A = {2,3,5,7}

B = {1, 2, 4, 8}

∴ A∪B = {1, 2, 3, 4, 5, 7, 8}

Properties:

i) A ∪ B = B ∪ A (Commutativity)

ii) (A ∪ B) ∪ C = A ∪ (B ∪ C)

(Associativity)

iii) A ∪ φ = A Identity for union

iv) A ∪ A = A Idempotent law

v) If A∪ A' = U

vi) If A⊂B then A∪B = B

vii) U∪A = U

viii) A⊂(A∪B), B⊂(A∪B)

3) Intersection of sets:

The intersection of two sets A and B is the

set of all elements which are both in A and

B is denoted by A∩B

Thus, A ∩ B = {x/x∈A and x∈B}

Sets relation function operation on set

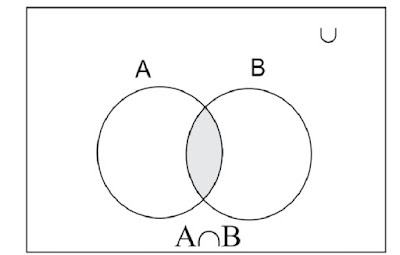
The shaded portion in Fig. 5.5 represents

the intersection of A and B i.e. A∩B

Ex. A={1,3,5,7,9}

B = {1,2,3,4,5,6,7,8}

Find A∩B.

Solution: A∩B = {1,3,5,7}

Ex. (Activity) : If A = {x/x∈N, x is a factor of 12}

B = {x/x∈N, x is a factor of 18}

Find A∩B

Solution:

A={ 1, 2, 3, 4 , 6, 12}

B = { 1, 2, 3, 6, 9, 18}

∴ A∩B = { 1, 2, 3, 6}

= common factors of 12 & 18

Ex. : A = {1,3,5,7,9}

B = {2,4,6,8, 10}, A∩B = ?

Solution :

∴ A∩B = { } = φ

If A∩B = φ, A and B are disjoint sets

Properties:

i) A∩B = B ∩A (Commutativity)

ii) (A ∩ B) ∩ C = A ∩ (B ∩ C)

(Associativity)

iii) φ∩ A = φ

iv) A ∩ A = A Idempotent law

v) A∩ A = ∅

vi) if A⊂B then A∩B =A

vii) U∩A = A (Identity for intersection)

viii) (A∩B) ⊂A, (A∩B) ⊂B

ix) a) A∩(B∪C) = (A∩B)∪ (A∩C)

b) A∪(B∩C) = (A∪B) ∩ (A∪C)

..... Distributivity

De Morgan's Laws:

For any two sets A and B

1) (A∪B)' = (A'∩B')

2) (A∩B)' = (A'∪B')

4) Difference of Sets:

Difference of set A and set B is the set of

elements which are in A but not in B and is

denoted by A-B, or A∩B'

The shaded portion in represents

Sets relation function operation on set

A-B. Thus, A-B = {x/x∈A, x∉B}

Similary B-A = {y/y∈B, y∉A}

Note:

i) A-B ⊆ A and B-A ⊆ B.

ii) The sets A-B, A∩B and B-A are mutually

disjoint sets, i.e. the intersection of any of

these two sets is the null (empty) set.

iii) A-B = A∩B' , B-A = A'∩B

iv) A∪B = (A-B)∪(A∩B) ∪ (B-A)

v) (A-B) ∪ (B-A) = A∆B is called symmetric

difference of sets A and B

Sets relation function operation on set

Sets relation function operation on set